这是我关于《轻松客观认识大模型系列》第二篇
五、什么是深度学习
深度学习可以在电路中加入电阻和门以外的元素,例如在电路的中间加入数学计算,将多个值相加或相乘后再向前传递电信号。但深度学习仍然使用相同的基本增量技术来猜测参数。
六、什么是语言模型
我们之前举的汽车例子中,我们试图让神经网络的行为与我们的数据一致。我们在询问是否可以创建一个电路,以类似于司机在相似情况下操作汽车的方式来操纵汽车。我们可以用同样的方式对待语言。我们可以查看人类编写的文本,思考是否可以创建一个电路,产生一个看起来很像人类倾向于产生的单词序列。现在,当我们看到单词时,我们的传感器就会触发,我们的输出机制也是单词。
我们在尝试做什么?我们正在尝试创建一个电路,给定一堆输入单词,猜测一个输出单词。例如:
“Once upon a __”
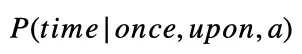
如果您不熟悉这个符号,不用担心。这只是数学术语,意味着给定“once”,“upon”和“a”这些单词,单词“time”的概率(P)。我们希望一个好的语言模型比单词“armadillo”产生更高的概率。
我们可以将其推广到:
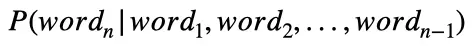
这句话的意思是计算在给定前面所有单词(从第一个单词到第n-1个单词)的情况下,序列中第n个单词出现的概率。但让我们回到一点。想想那种有敲打臂的老式打字机。

除了不是每个字母都有一个不同的敲击臂之外,我们为每个单词配备一个敲击器。如果英语有50,000个单词,那么这是一个庞大的打字机!
不同于汽车的网络,想象一个类似的网络,除了我们电路的顶部有50,000个输出连接到敲击器臂,每个单词对应一个敲击器。相应地,我们将有50,000个传感器,每个传感器检测不同输入单词的存在。因此,最终我们所做的是选择一个电信号最强的敲击臂,这就是填空的单词。
现在,如果我想要制作一个简单的电路,以输入一个单词并产生一个单词输出,我必须制作一个具有50,000个传感器和50,000个输出的电路(每个单词一个)。我只需将每个传感器连接到每个敲击臂,总计需要 50,000 x 50,000 = 25亿根导线。

这真是一个庞大的网络工程!
更糟糕的是,如果我想做“Once upon a ___”这个例子,我需要感应到三个输入位置的每个单词。我需要 50,000 x 3 = 150,000 个传感器。连接到 50,000 个打字臂,就需要 150,000 x 50,000 = 7.5 十亿个电线。截至2023年,大多数大型语言模型可以输入4,000个单词,最大的可以输入32,000个单词。我的眼睛都要花了。

我们需要一些技巧来解决这个问题。我们将逐步进行。
6.1 编码器
我们要做的第一件事是将电路分为两个电路,一个称为编码器,另一个称为解码器。我们的一个洞见是,许多单词的意思大致相同。考虑以下短语:
The king sat on the ___
The queen sat on the ___
The princess sat on the ___
The regent sat on the ___
实际上,很多单词的意思是差不多的。例如,“国王”,“女王”和“皇帝”都有关于皇室或权力的意思。因此,我们可以使用一个中间的东西(比如“皇权”)来表示这些单词所代表的权力的概念。这样,我们只需要考虑哪些单词的意思是差不多的,然后决定给这个中间的东西(“皇权”)多少电信号能量。这就相当于把所有的“皇权”相关的单词都归到同一个类别里。这个过程就是编码。
因此,我们要做的是建立一个电路,它将50,000个词的传感器映射到一些更小的输出集中,例如256个而不是50,000个。而且,我们不仅能够触发一个打字臂,而且能够同时触发一堆打字臂。每个可能的打字臂组合都可以表示不同的概念(如“皇室”或“有盔甲的哺乳动物”)。这256个输出将使我们能够表示2²⁵⁶ = 1.15 x 10⁷⁸个概念。实际上,还有更多的可能性,因为就像汽车示例中我们可以将刹车部分按下,每个256个输出不仅可以是1.0或0.0,还可以是它们之间的任何数字。因此,也许更好的比喻是所有256个打字臂都被按下,但每个打字臂按下的力度不同。
好的…以前每个单词需要一个50,000个传感器之一触发。现在,我们已经将一个触发的传感器和49,999个关闭的传感器缩减到256个数字。因此,“king”可能是[0.1,0.0,0.9,…,0.4],“queen”可能是[0.1,0.1,0.9,…,0.4],它们几乎相同。我将这些数字列表称为编码(也称为隐藏状态,出于历史原因,但我不想解释这一点,因此我们将坚持使用编码)。我们称将50,000个传感器压缩为256个输出的电路为编码器。它看起来像这样:

6.2 解码器
但是编码器并不能告诉我们下一个单词应该是什么。因此,我们将编码器与解码器网络配对。解码器是另一个电路,它接受编码所需的256个数字,并激活原始的50,000个撞击臂之一,以产生下一个单词。然后,我们将选择输出电流最高的单词。下面是解码器的示意图:

6.3 编码器和解码器一起使用
这是编码器和解码器一起工作形成的一个大型神经网络:
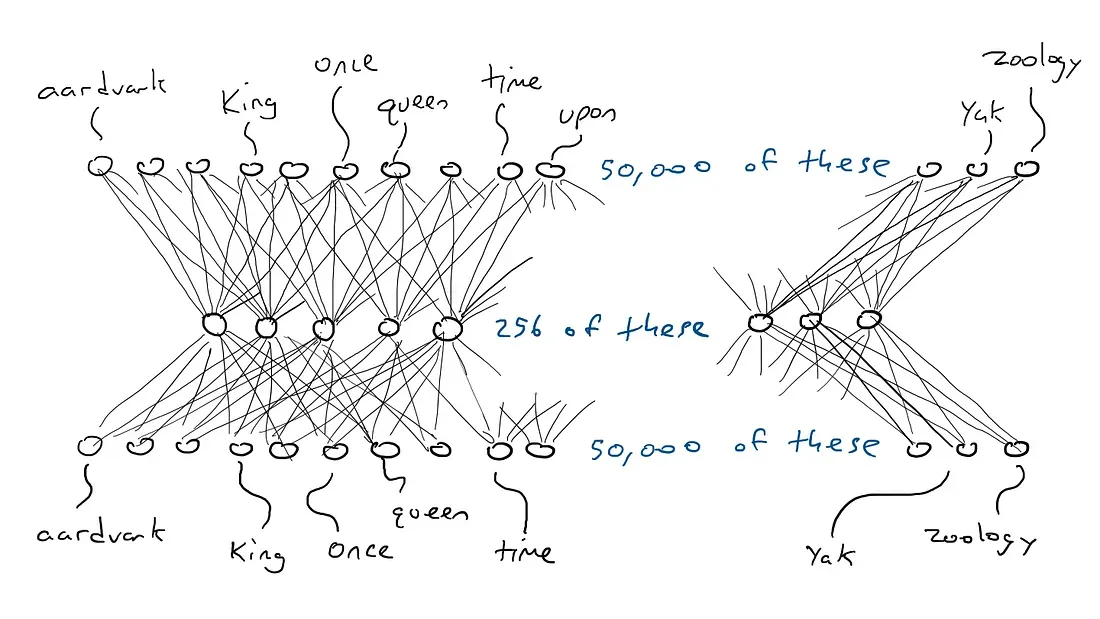
顺便提一句,对于单词输入到单词输出的编码,只需要 (50,000 x 256) x 2 = 25,600万个参数。看起来效果很不错。
这个例子是针对一个单词输入和一个单词输出的情况,如果我们想读取n个单词,那么输入就是50,000 x n,编码输出就是256 x n。
但是为什么会起作用呢?通过强制使50,000个单词适合一小组数字,我们迫使网络做出妥协并将可能触发相同输出猜测的单词组合在一起。这很像文件压缩。当您压缩文本文档时,会得到一个不可读的较小文档。但是您可以解压文档并恢复原始可读文本。这是因为压缩程序使用简写符号替换某些单词模式。然后在解压缩时,它知道该用哪个文本来替换简写符号。我们的编码器和解码器电路学习了一种电阻器和门的配置,可以对单词进行压缩和解压缩。
6.4 自我监督
我们怎么知道每个单词的编码最好的配置是什么?换句话说,我们怎么知道“king”和“queen”的编码应该相似而不是与“armadillo”相似呢?
想象一下,有一个编码器-解码器网络,应该输入一个单词(50,000个传感器)并产生完全相同的单词作为输出。这个做法不是很好,但对于接下来要讲的内容非常有教育意义。

输入单词“king”,一个传感器会发送电信号通过编码器,部分激活256个编码中的值。如果编码正确,解码器就会将最高电信号发送给相同的单词“king”。很简单吧?但不要这么快下结论。我同样可能会看到拥有最高激活能量的是“armadillo”这个词的撞击臂。假设“king”的撞击臂得到0.051的电信号,而“armadillo”的撞击臂得到0.23的电信号。实际上,我甚至不关心“armadillo”的值是多少。我只需要看“king”的输出能量,就知道它不是1.0。1.0和0.051之间的差异是误差(也称为损失),我可以使用反向传播对解码器和编码器进行一些改变,以便在下次看到单词“king”时生成略微不同的编码。
我们对所有的单词都这样做。编码器必须做出妥协,因为 256 远远小于 50,000。也就是说,有些单词在中间的激活能量组合上将不得不使用相同的编码。因此,当有选择的时候,编码器会希望“king”和“queen”的编码几乎相同,而“armadillo”的编码则非常不同。这将使解码器更容易通过只查看 256 个编码值来猜测单词。如果解码器看到了一组特定的 256 个值,并猜测“king”的概率是 0.43,而“queen”的概率是 0.42,只要“king”和“queen”获得了最高的电信号,而其他 49,998 个触发器的数字都比它们小,我们就会满意。换句话说,如果神经网络在“king”和“queen”之间感到困惑,我们可能会更容忍,而如果网络在“king”和“armadillo”之间感到困惑,我们就不能容忍了。
我们说神经网络是自我监督的,因为与汽车示例不同,我们不需要收集单独的数据来测试输出。我们只需将输出与输入进行比较,而不需要单独为输入和输出收集数据。
6.5 掩码语言模型
如果上面的思想实验看起来有些简单,那是因为它是构建掩码语言模型的基石。掩码语言模型的想法是输入一系列单词并生成一系列单词,其中输入和输出中的一个单词被遮挡掉了。
The [MASK] sat on the throne.
这个网络要猜测所有的单词,但是猜测未被覆盖的单词很容易。我们实际上只关心网络对遮挡单词的猜测。也就是说,对于输出中的每个单词,我们都有50,000个打击臂。我们只看覆盖单词的这些打击臂。
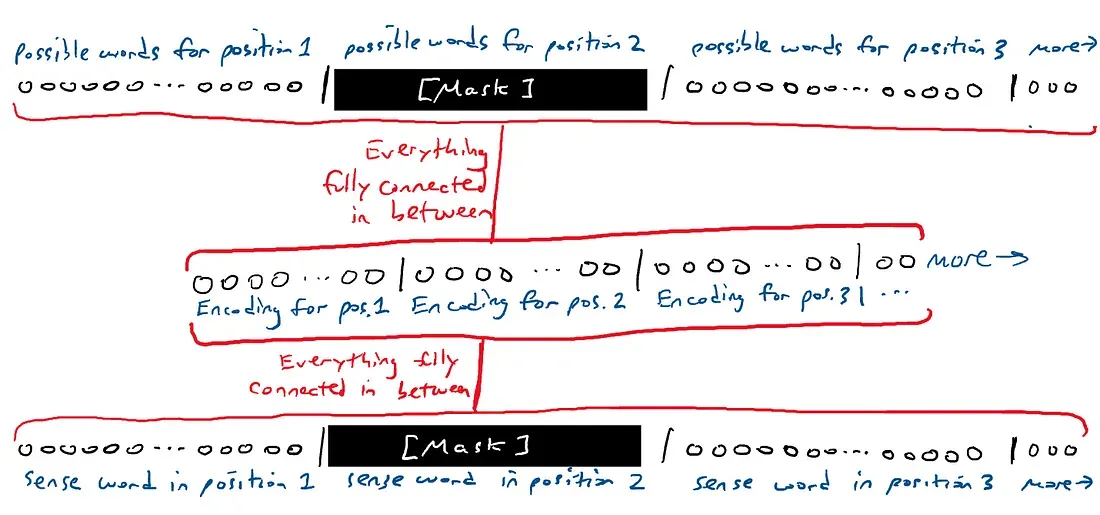
我们可以移动掩码并让网络在不同位置猜测不同的单词。
一种特殊类型的掩码语言模型仅在末尾有掩码。这被称为生成模型,因为它要猜测的掩码始终是序列中的下一个单词,这相当于生成下一个单词,就好像下一个单词不存在一样。就像这样:
The [MASK]
The queen [MASK]
The queen sat [MASK]
The queen sat on [MASK]
The queen sat on the [MASK]
我们也称之为自回归模型。回归这个词听起来不太好,但回归只是试图理解事物之间的关系,比如输入的单词和应该输出的单词之间的关系。Auto意味着“自己”。自回归模型是自我预测的。它预测一个单词,然后使用这个单词来预测下一个单词,以此类推。这对后面的一些有趣的推论有一定的影响,我们稍后会回到这个问题。